Gridea

温故而知新

首页 归档 标签 关于

洛谷 P3369 题解

2020-03-17 15 min read # 题解

什么？！21页题解竟然没有一个人写 AVL 树，于是本蒟蒻就写一篇 AVL 树的题解。当然， AVL 树可能会比较难，而且常数较大，但如果有比较多的插入和删除 AVL 树就会有优势。

我们都知道，普通的二叉搜索树的插入、删除、查找期望时间复杂度为 O(log⁡2n)O(\log_2 n)，但在特殊构造的数据中时间复杂度为 O(n)O(n)，如图所示。

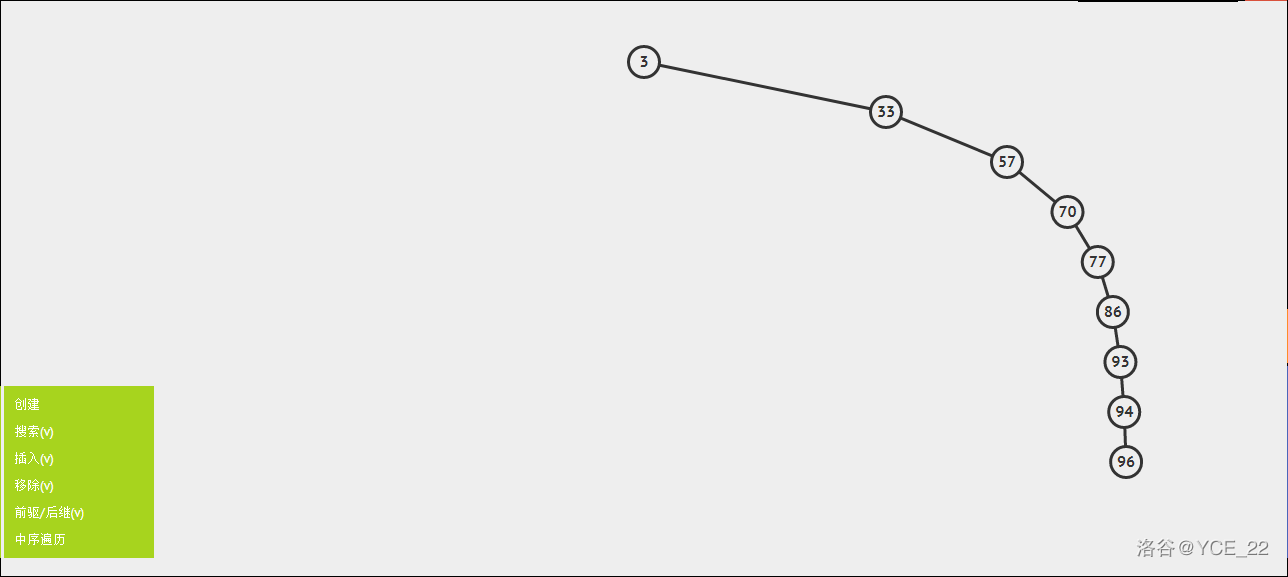
但是，AVL 树有一个性质，就是两棵子树的高度差的绝对值不超过1，所以期望时间复杂度为 O(log⁡2n)O(\log_2 n)，最坏情况下时间复杂度为 O(log⁡ϕn)O(\log_\phi n)，如图所示。

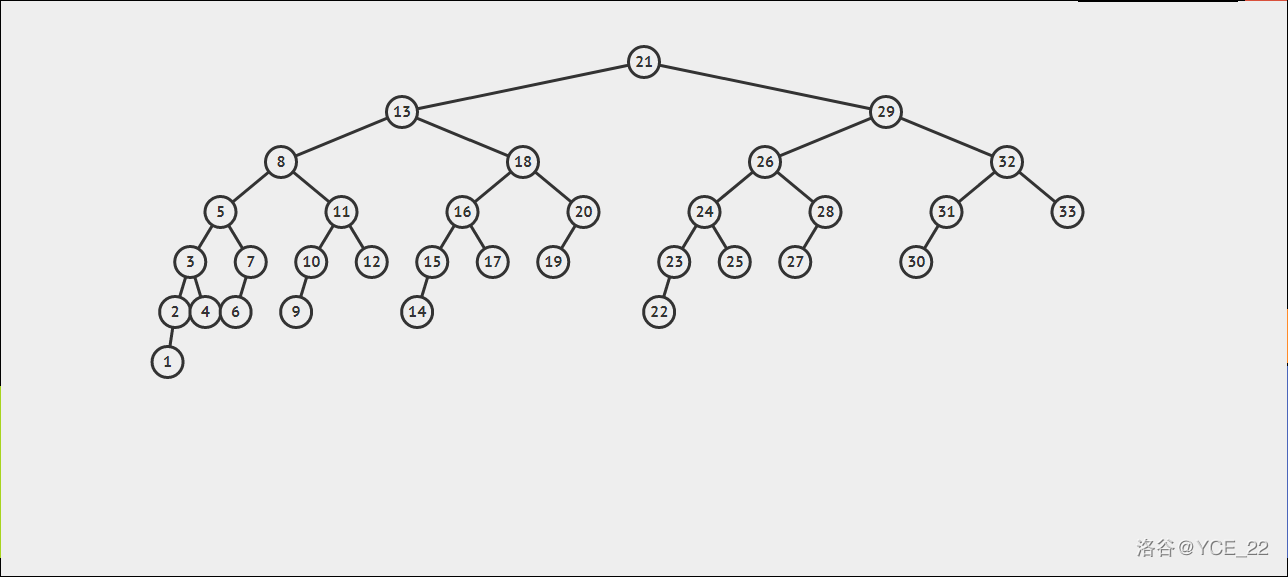
由于 log⁡ϕ2=1.44\log_\phi2=1.44，所以最坏情况的时间复杂度为 O(log⁡21.44n)O(\log_2^{1.44} n)，时间复杂度不高。

做法：

基本的节点定义：

struct AVLnode;
typedef AVLnode* AVLtree;
struct AVLnode {
	int data, high;//权值，树高
	int freq, size;//频数，大小
	AVLtree ls, rs;//左子，右子
	AVLnode(): data(0), high(1), freq(1), size(1), ls(NULL), rs(NULL){}
	AVLnode(int a): data(a), high(1), freq(1), size(1), ls(NULL), rs(NULL){}//初始化
};

获取及更新树高，大小：

为了防止因访问空节点而导致 RE，所以要特定函数来获取及更新

inline int GetSize(AVLtree p) {//获取大小
	if (p == NULL) return 0;
	return p->size;
}
inline int GetHigh(AVLtree p) {//获取树高
	if (p == NULL) return 0;
	return p->high;
}
inline void update(AVLtree& p) {//更新节点
	p->size = GetSize(p->ls) + GetSize(p->rs) + p->freq;
	p->high = max(GetHigh(p->ls), GetHigh(p->rs)) + 1;
}

左右旋转：

AVL 树的旋转方式有四种：左左，右右，左右，右左。

左左：

假如有这样一颗二叉树，如图所示。

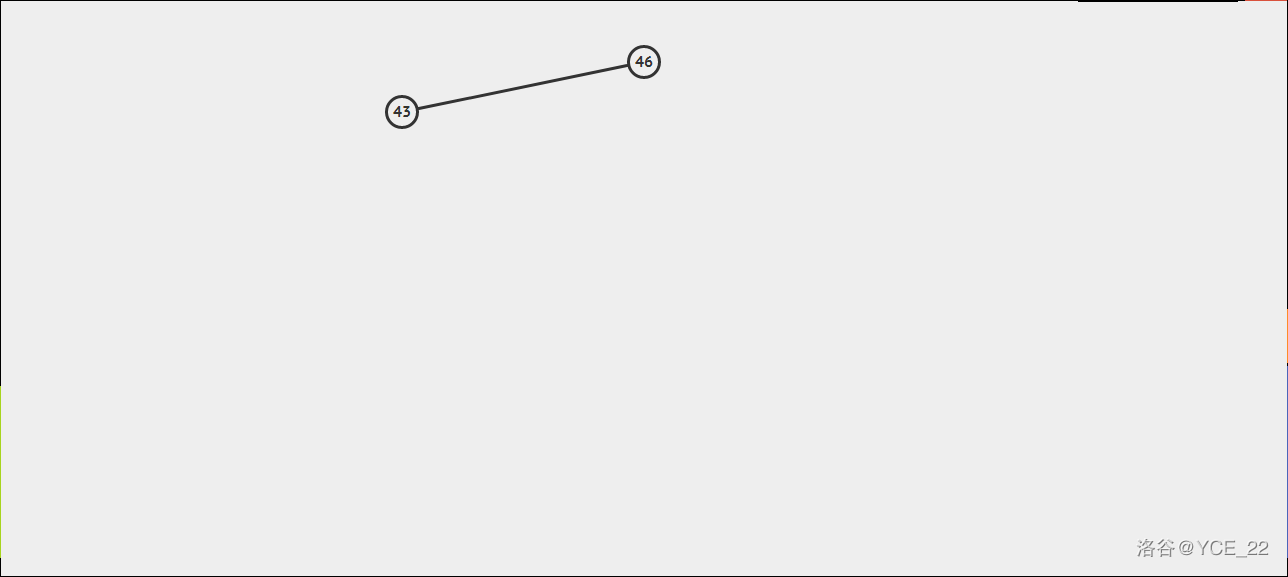
现在要插入21，则步骤如下（注意右下角的字）:


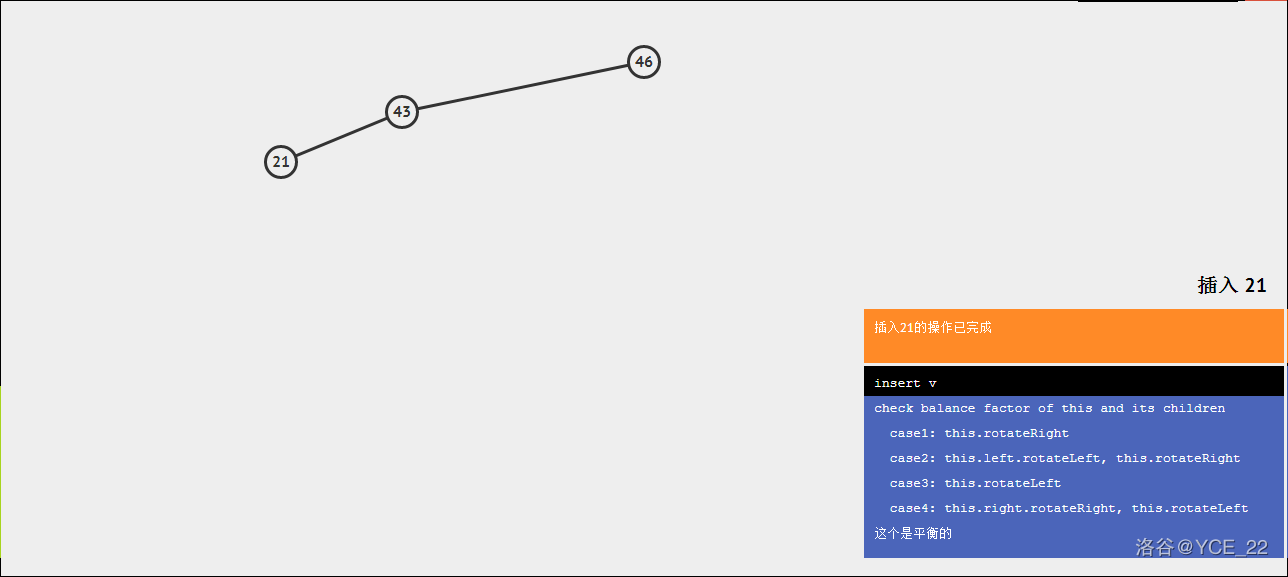
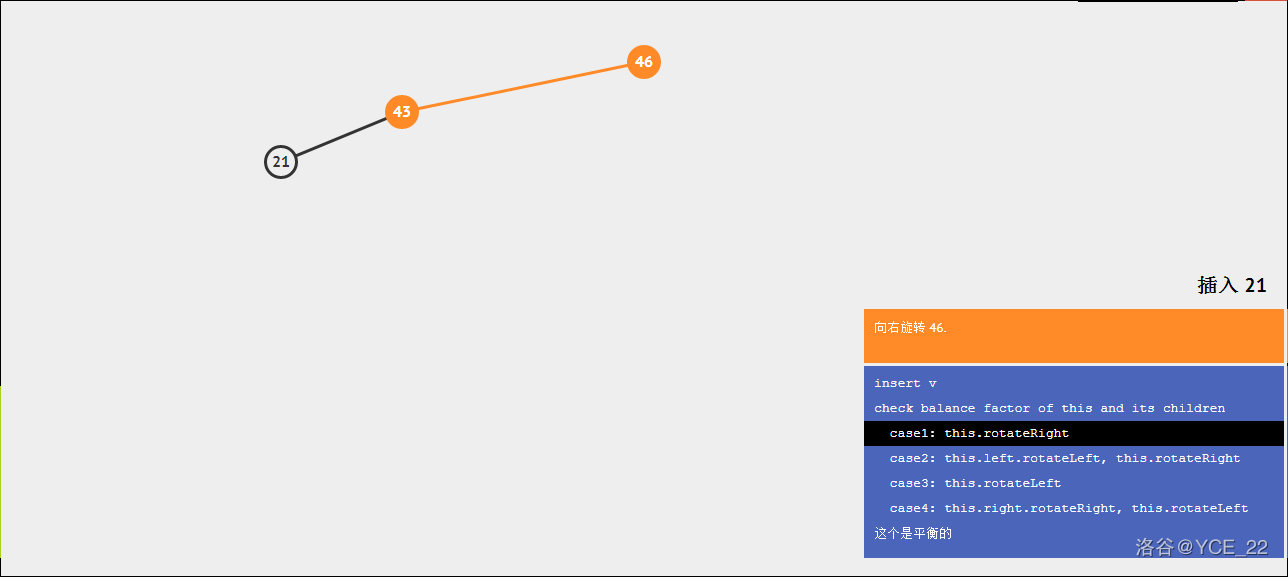
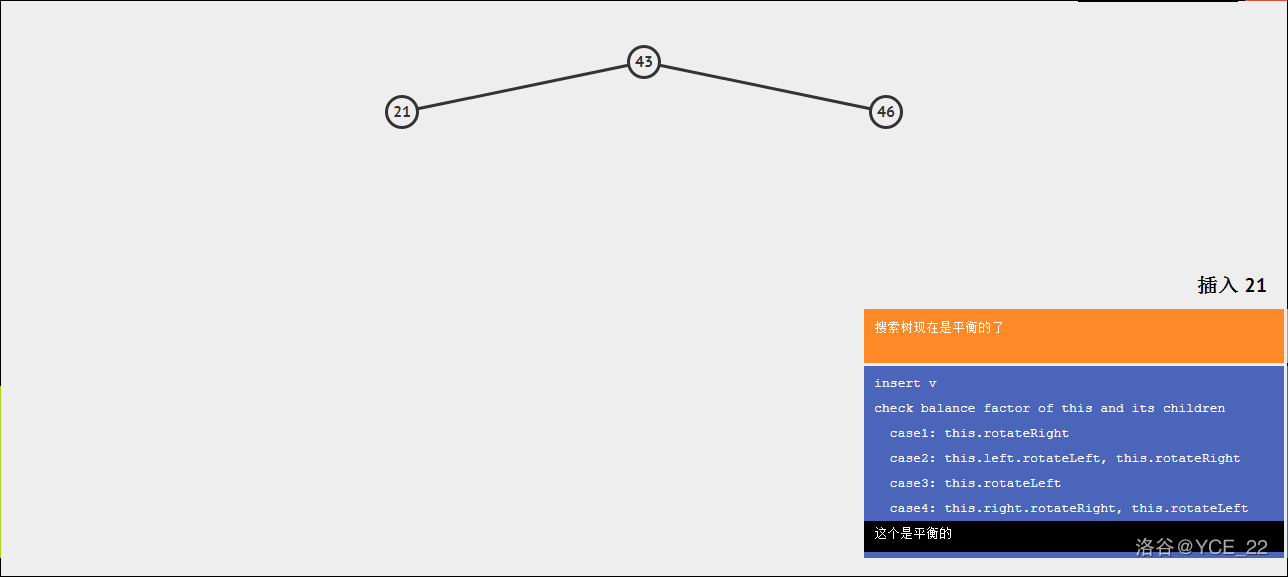
inline void LeftPlus(AVLtree& p) {
	AVLtree q;
	q = p->ls;
	p->ls = q->rs;
	q->rs = p;
	update(p);
	update(q);
	p = q;
}

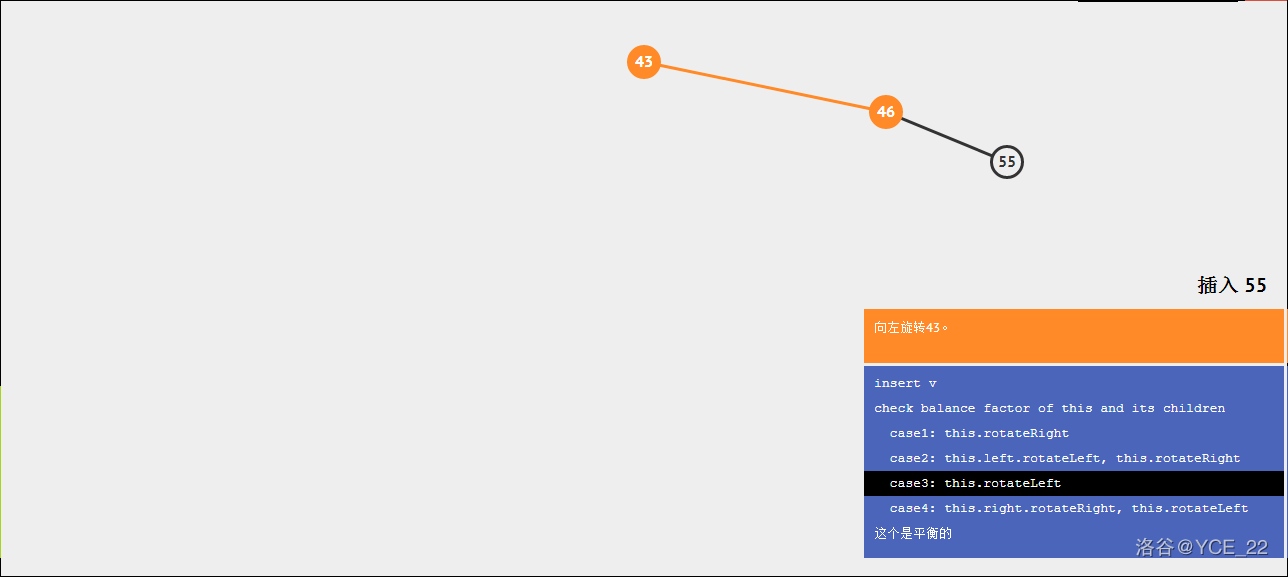
右右：

假如有这样一颗二叉树，如图所示。

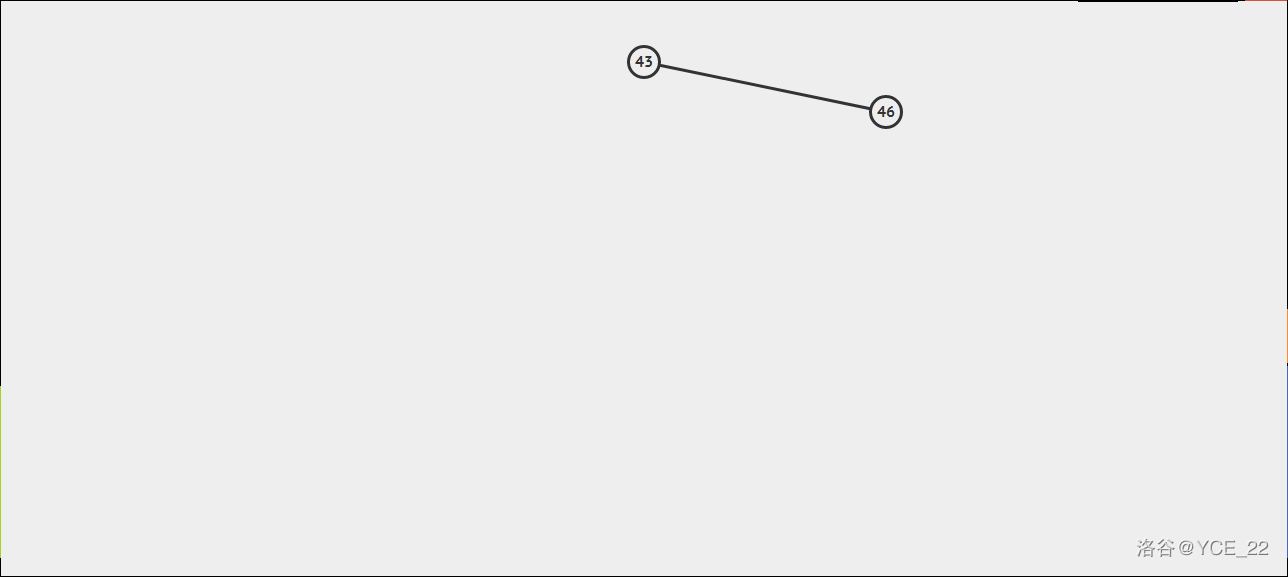
现在要插入55，则步骤如下：


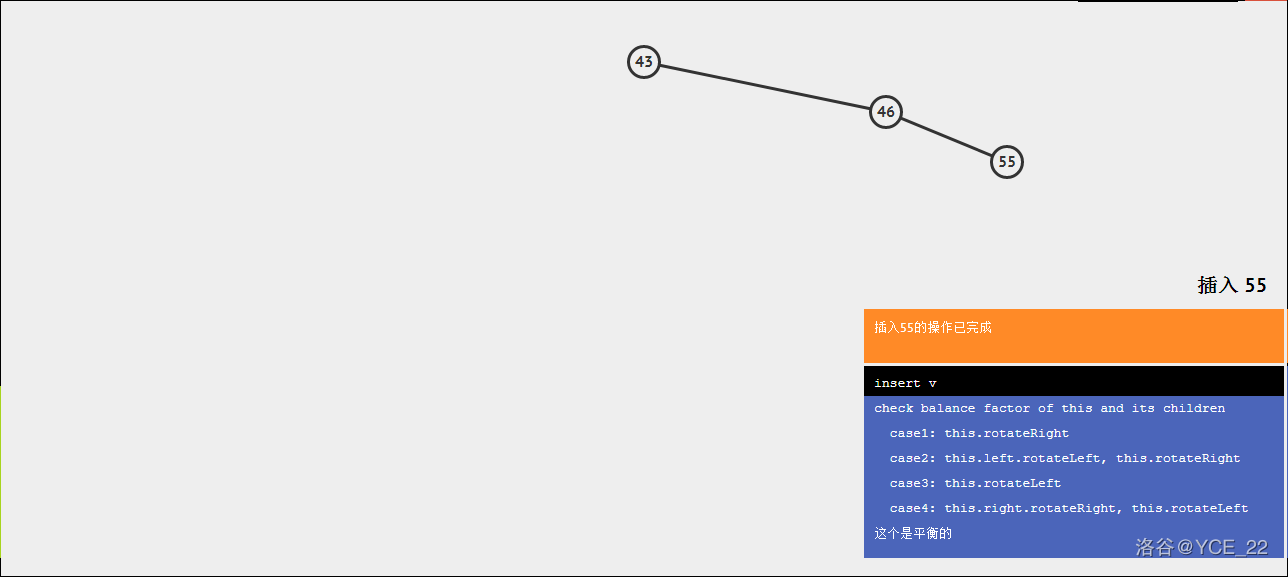
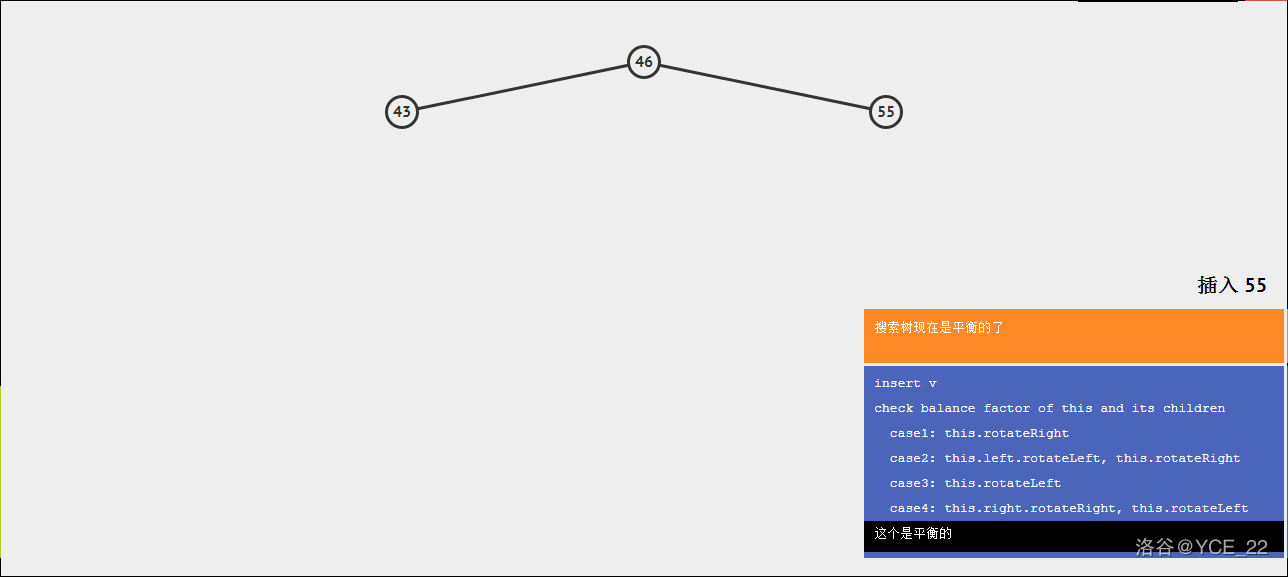
inline void RightPlus(AVLtree& p) {
	AVLtree q;
	q = p->rs;
	p->rs = q->ls;
	q->ls = p;
	update(p);
	update(q);
	p = q;
}

左右及右左：

左右要先把这颗二叉树向右旋转变成左左，再左旋；右左反之。

inline void LeftRight(AVLtree& p) {//左右
	RightPlus(p->ls);
	LeftPlus(p);
}
inline void RightLeft(AVLtree& p) {//右左
	LeftPlus(p->rs);
	RightPlus(p);
}

中序遍历(本题不需要，但可当做调试语句)：

inline void OutPut(AVLtree p) {
	if (p == NULL) return;
	OutPut(p->ls);
	for (int i = 1; i <= p->freq; ++i)
		write(p->data), putchar(32);
	OutPut(p->rs);
}
inline void output() {//主程序可以更简洁，下同
	OutPut(root);
}

插入：

先按照普通二叉搜索树的方式插入，再进行调整。

inline void Insert(AVLtree &p, int x) {
	if (p == NULL) {
		p = new AVLnode(x);//没有这个节点，直接插入一个
		return;
	}
	if (p->data == x) {//如果已经有这个树了，直接增加这个数的频率，更新这个节点即可
		++(p->freq);
		update(p);
		return;
	}
	if (p->data > x) {//往左子树插入，左子树可能偏高
		Insert(p->ls, x), update(p);
		if (GetHigh(p->ls) - GetHigh(p->rs) == 2) {
			if (x < p->ls->data)
				LeftPlus(p);//左左
			else
				LeftRight(p);//左右
		}
	}
	else {//往右子树插入，右子树可能偏高
		Insert(p->rs, x), update(p);
		if (GetHigh(p->rs) - GetHigh(p->ls) == 2) {
			if (x > p->rs->data)
				RightPlus(p);//右右
			else
				RightLeft(p);//右左
		}
	}
	update(p);//别忘记更新
}
inline void insert(int x) {
	Insert(root, x);
}

删除：

先按照普通二叉搜索树的方式删除，再进行调整。

inline void Erase(AVLtree& p, int x) {
	if (p == NULL) return;//找不到这个树，直接返回
	if (p->data > x) {//删左子树的数，右子树可能偏高
		Erase(p->ls, x), update(p);
		if (GetHigh(p->rs) - GetHigh(p->ls) == 2) {
			if (GetHigh(p->rs->rs) >= GetHigh(p->rs->ls))//一定要加等号，同下，就是因为这个，本蒟蒻92分调了55分钟！
				RightPlus(p);
			else
				RightLeft(p);
		}
	}
	else if(p->data < x) {
		Erase(p->rs, x), update(p);
		if (GetHigh(p->ls) - GetHigh(p->rs) == 2) {
			if (GetHigh(p->ls->ls) >= GetHigh(p->ls->rs))
				LeftPlus(p);
			else
				LeftRight(p);
		}
	}
	else {
		if (p->freq > 1) {//如果这个数的频率大于1，那么直接减去一个就可以了
			--(p->freq);
			update(p);
			return;
		}
		if (p->ls && p->rs) {//左右子树都有
			AVLtree q = p->rs;//找这个数的后继
			while (q->ls) q = q->ls;
			p->freq = q->freq;
			p->data = q->data, q->freq = 1;//把q节点提上来
			Erase(p->rs, q->data);//这个节点肯定少于2个子树了，直接删除
			update(p);//别忘记更新
			if (GetHigh(p->ls) - GetHigh(p->rs) == 2) {
				if (GetHigh(p->ls->ls) >= GetHigh(p->ls->rs))
					LeftPlus(p);
				else
					LeftRight(p);
			}
		}
		else {//如果只有一个子树，直接把这个节点的子树提上来即可，不需要更新
			AVLtree q = p;
			if (p->ls) p = p->ls;
			else if (p->rs) p = p->rs;
			else p = NULL;
			delete q;
			q = NULL;
		}
	}
	if (p == NULL) return;//注意这里还要判断，否则可能会RE
	update(p);//最后更新一下
}
inline void erase(int x) {
	Erase(root, x);
}

根据数值找排名：

inline int get_rank(AVLtree p, int val) {
	if (p->data == val) return GetSize(p->ls) + 1;//如果这个节点就是要找的数字，返回左子树的大小加1
	if (p->data > val) return get_rank(p->ls, val);//如果这个节点大于要找的数字，往左找
	return get_rank(p->rs, val) + GetSize(p->ls) + p->freq;//往右找，返回值要加上左子树的大小和这个节点数出现的频数
}
inline int GetRank(int val) {
	return get_rank(root, val);
}

根据排名找数值：

inline int get_val(AVLtree p, int rank) {
	if (GetSize(p->ls) >= rank) return get_val(p->ls, rank);//如果左子树的大小不小于排名，往左找
	if (GetSize(p->ls) + p->freq >= rank) return p->data;//如果左子树的大小加上这个节点数值出现的频数不小于排名，返回这个数值
	return get_val(p->rs, rank - GetSize(p->ls) - p->freq);//往右找，主要排名要减去左子树的大小和这个节点数值出现的频数
}
inline int GetVal(int rank) {
	return get_val(root, rank);
}

找前驱后继：

inline int GetPrev(int val) {//找前驱
	AVLtree ans = new AVLnode(-1LL << 42), p = root;//从根节点开始找，初始答案赋最小值
	while (p) {//如果p节点不为空，则一直找
		if (p->data == val) {
			if (p->ls) {//如果找到这个数了，先找这个数的左子树，再一直往右找
				p = p->ls;
				while (p->rs)
					p = p->rs;
				ans = p;
			}
			break;
		}
		if (p->data < val && p->data > ans->data) ans = p;//如果遇到一个比这个值小但大于当前答案的值的话，把答案赋给ans
		p = p->data < val ? p->rs : p->ls;
	}
	return ans->data;
}
inline int GetNext(int val) {//找后继，与找前驱类似
	AVLtree ans = new AVLnode(1LL << 42), p = root;
	while (p) {
		if (p->data == val) {
			if (p->rs) {
				p = p->rs;
				while (p->ls)
					p = p->ls;
				ans = p;
			}
			break;
		}
		if (p->data > val && p->data < ans->data) ans = p;
		p = p->data < val ? p->rs : p->ls;
	}
	return ans->data;
}

完整代码如下(注释前面有了，就不写了)：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 100000 + 10;
template<class T> inline void read(T &x) {
	char c = 0;
	int f = x = 0;
	while (c < 48 || c > 57) {
		if (c == '-')
			f = 1;
		c = getchar();
	}
	while (c > 47 && c < 58) x = (x << 3)+(x << 1)+(c & 15), c = getchar();
	if (f) x = -x;
}
template<class T,class... Args> inline void read(T &x, Args&... args) {
	read(x), read(args...);
}
template<class T> inline void write(T x) {
	if (x < 0) {
		putchar(45);
		write(-x);
		return;
	}
	if (x > 9) write(x / 10);
	putchar((x % 10) | 48);
}
struct AVLnode;
typedef AVLnode* AVLtree;
struct AVLnode {
	int data, high;
	int freq, size;
	AVLtree ls, rs;
	AVLnode(): data(0), high(1), freq(1), size(1), ls(NULL), rs(NULL){}
	AVLnode(int a): data(a), high(1), freq(1), size(1), ls(NULL), rs(NULL){}
};
inline int GetSize(AVLtree p) {
	if (p == NULL) return 0;
	return p->size;
}
inline int GetHigh(AVLtree p) {
	if (p == NULL) return 0;
	return p->high;
}
struct AVL {
	AVLtree root;
	inline void update(AVLtree& p) {
		p->size = GetSize(p->ls) + GetSize(p->rs) + p->freq;
		p->high = max(GetHigh(p->ls), GetHigh(p->rs)) + 1;
	}
	inline void LeftPlus(AVLtree& p) {
		AVLtree q;
		q = p->ls;
		p->ls = q->rs;
		q->rs = p;
		update(p);
		update(q);
		p = q;
	}
	inline void RightPlus(AVLtree& p) {
		AVLtree q;
		q = p->rs;
		p->rs = q->ls;
		q->ls = p;
		update(p);
		update(q);
		p = q;
	}
	inline void LeftRight(AVLtree& p) {
		RightPlus(p->ls);
		LeftPlus(p);
	}
	inline void RightLeft(AVLtree& p) {
		LeftPlus(p->rs);
		RightPlus(p);
	}
	inline void OutPut(AVLtree p) {
		if (p == NULL) return;
		OutPut(p->ls);
		for (int i = 1; i <= p->freq; ++i)
			write(p->data), putchar(32);
		OutPut(p->rs);
	}
	inline void output() {
		OutPut(root);
	}
	inline void Insert(AVLtree &p, int x) {
		if (p == NULL) {
			p = new AVLnode(x);
			return;
		}
		if (p->data == x) {
			++(p->freq);
			update(p);
			return;
		}
		if (p->data > x) {
			Insert(p->ls, x), update(p);
			if (GetHigh(p->ls) - GetHigh(p->rs) == 2) {
				if (x < p->ls->data)
					LeftPlus(p);
				else
					LeftRight(p);
			}
		}
		else {
			Insert(p->rs, x), update(p);
			if (GetHigh(p->rs) - GetHigh(p->ls) == 2) {
				if (x > p->rs->data)
					RightPlus(p);
				else
					RightLeft(p);
			}
		}
		update(p);
	}
	inline void insert(int x) {
		Insert(root, x);
	}
	inline void Erase(AVLtree& p, int x) {
		if (p == NULL) return;
		if (p->data > x) {
			Erase(p->ls, x), update(p);
			if (GetHigh(p->rs) - GetHigh(p->ls) == 2) {
				if (GetHigh(p->rs->rs) >= GetHigh(p->rs->ls))
					RightPlus(p);
				else
					RightLeft(p);
			}
		}
		else if(p->data < x) {
			Erase(p->rs, x), update(p);
			if (GetHigh(p->ls) - GetHigh(p->rs) == 2) {
				if (GetHigh(p->ls->ls) >= GetHigh(p->ls->rs))
					LeftPlus(p);
				else
					LeftRight(p);
			}
		}
		else {
			if (p->freq > 1) {
				--(p->freq);
				update(p);
				return;
			}
			if (p->ls && p->rs) {
				AVLtree q = p->rs;
				while (q->ls) q = q->ls;
				p->freq = q->freq;
				p->data = q->data, q->freq = 1;
				Erase(p->rs, q->data);
				update(p);
				if (GetHigh(p->ls) - GetHigh(p->rs) == 2) {
					if (GetHigh(p->ls->ls) >= GetHigh(p->ls->rs))
						LeftPlus(p);
					else
						LeftRight(p);
				}
			}
			else {
				AVLtree q = p;
				if (p->ls) p = p->ls;
				else if (p->rs) p = p->rs;
				else p = NULL;
				delete q;
				q = NULL;
			}
		}
		if (p == NULL) return;
		update(p);
	}
	inline void erase(int x) {
		Erase(root, x);
	}
	inline int get_val(AVLtree p, int rank) {
		if (GetSize(p->ls) >= rank) return get_val(p->ls, rank);
		if (GetSize(p->ls) + p->freq >= rank) return p->data;
		return get_val(p->rs, rank - GetSize(p->ls) - p->freq);
	}
	inline int GetVal(int rank) {
		return get_val(root, rank);
	}
	inline int get_rank(AVLtree p, int val) {
		if (p->data == val) return GetSize(p->ls) + 1;
		if (p->data > val) return get_rank(p->ls, val);
		return get_rank(p->rs, val) + GetSize(p->ls) + p->freq;
	}
	inline int GetRank(int val) {
		return get_rank(root, val);
	}
	inline int GetPrev(int val) {
		AVLtree ans = new AVLnode(-1LL << 42), p = root;
		while (p) {
			if (p->data == val) {
				if (p->ls) {
					p = p->ls;
					while (p->rs)
						p = p->rs;
					ans = p;
				}
				break;
			}
			if (p->data < val && p->data > ans->data) ans = p;
			p = p->data < val ? p->rs : p->ls;
		}
		return ans->data;
	}
	inline int GetNext(int val) {
		AVLtree ans = new AVLnode(1LL << 42), p = root;
		while (p) {
			if (p->data == val) {
				if (p->rs) {
					p = p->rs;
					while (p->ls)
						p = p->ls;
					ans = p;
				}
				break;
			}
			if (p->data > val && p->data < ans->data) ans = p;
			p = p->data < val ? p->rs : p->ls;
		}
		return ans->data;
	}
};
int n, x, opt;
AVL a;
signed main() {
	read(n);
	for (int i = 1; i <= n; ++i) {
		read(opt, x);
		switch(opt) {
			case 1: a.insert(x); break;
			case 2: a.erase(x); break;
			case 3: write(a.GetRank(x)), putchar(10); break;
			case 4: write(a.GetVal(x)), putchar(10); break;
			case 5: write(a.GetPrev(x)), putchar(10); break;
			case 6: write(a.GetNext(x)), putchar(10); break;
		}
	}
	return 0;
}
Powered by Gridea RSS