洛谷 P6182 题解
推销一下我的新博客(但图片可能显示不了):https://yce3216037.github.io/post/luo-gu-p6182-ti-jie/
本人想看一下洛谷新增的题目,结果就被我切了,而且是本题首A。如果这一道题只有前两个操作,那么这道题目就是一道很水的模拟题,直接用栈就可以了。然而,有了第三个操作,那么就有点难了,这个我称它为“可持久化栈”。有一种朴素的做法,就是在前两个操作的时候,直接复制上一次的栈的结果,遇到第三种操作,就复制第 次操作的结果,因为说的是第 次操作前,而不是第 次操作后,这样,样例模拟如下(为了方便,一开始来一个编号为 的奶牛):
0 :-1
1 :-1 5
2 :-1 5 3
3 :-1 5 3 7
4 :-1 5 3
5 :-1 5
6 :-1 5 2
7 :-1 5 3 7
8 :-1 5 3 7 4
9 :-1 5 3 7
10:-1 5 2
11:-1 5
12:-1
但是,这样操作的时间复杂度为 ,空间复杂度也为 ,对于 的数据来说,不管从时间还是从空间上来说,都会炸,所以,需要有一个更优的方法。这就要用到我新创的“可持久化栈”了。
如何实现这个“可持久化栈”呢?我画一个图来模拟一下(图略丑,且有点多,见谅),由于我是先画完再截图的,所以会有多余的线段:
初始状态(这时候为了减少边界条件判断,还需要再加一个虚拟奶牛,编号任意):

第1步,插入5号奶牛,直接在上一次的操作后添加一头5号奶牛即可:
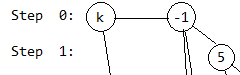
第2步,插入3号奶牛,和第1步类似:
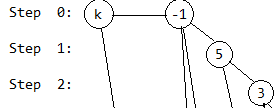
第3步,插入7号奶牛,和第1步类似:
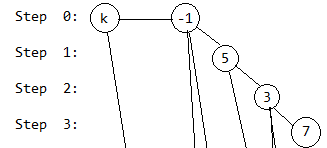
第4步,去掉7号奶牛,将在上一次操作的倒数第二头奶牛加在该奶牛的前一个奶牛后面,这样即可去掉最后一头奶牛:
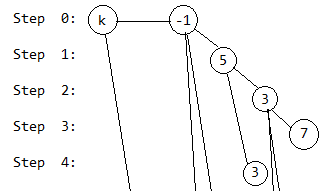
第5步,回到第4次操作前,将第2次操作后的队尾的奶牛加在该奶牛的前一个奶牛后面,即可忽略2至4步:
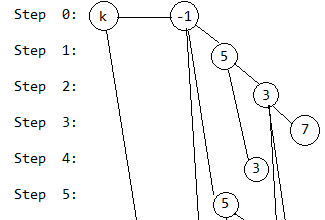
第6步,插入2号奶牛,和第1步类似:
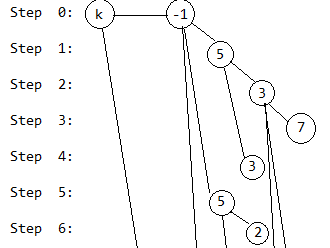
第7步,回到第4次操作前,和第5步类似:
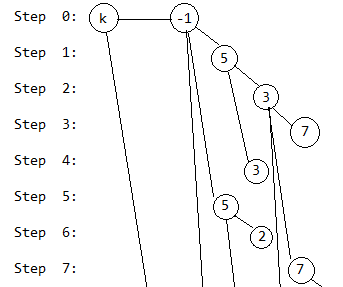
第8步,插入4号奶牛,和第1步类似:
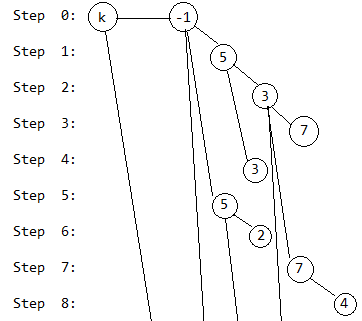
第9步,去掉4号奶牛,和第4步类似:
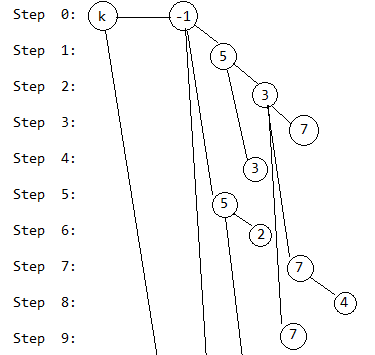
第10步,回到第7次操作前,和第5步类似:
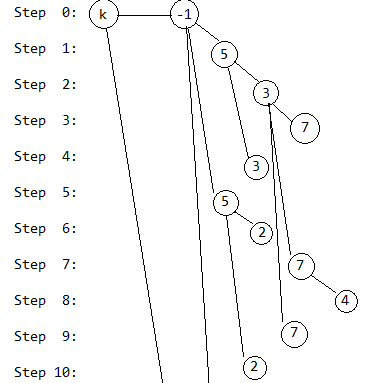
第11步,去掉2号奶牛,和第4步类似:
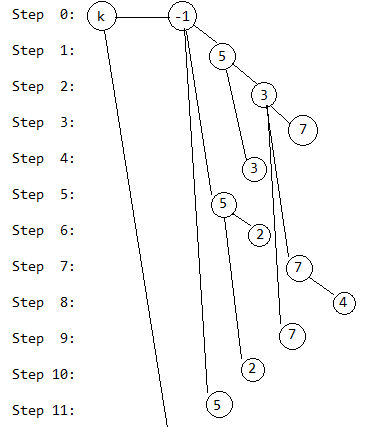
第12步,去掉5号奶牛,和第4步类似:
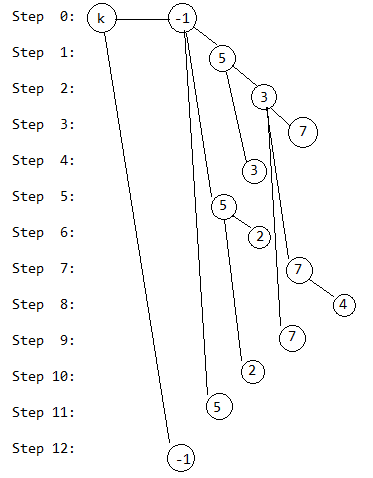
由于我想给大家介绍一下指针版如何实现装X,我写一个指针版的。
代码如下:
#include<cstdio>
using namespace std;
const int N = 80000 + 10;
FILE *fin, *fout;
inline int read(int &x) {//快读
char c = 0; int f = x = 0;
while (c < 48 || c > 57) {
if (c == -1) return 0;
if (c == '-') f = 1; c = fgetc(fin);
}
while (c > 47 && c < 58) x = (x << 3) + (x << 1) + (c & 15), c = fgetc(fin);
if (f) x = -x; return 1;
}
inline int read(char &c) {
c = 0; while (c == 32 || c == 10 || c == 13 || c == 0) c = fgetc(fin);
if (c == -1) return 0; return 1;
}
inline int write(int x) {//快写
if (x < 0) return fputc(45, fout), write(-x);
if (x > 9) write(x / 10);
return fputc((x % 10) | 48, fout), 1;
}
inline int write(char c) {
return fputc(c, fout), 1;
}
template<class T, class... Args> inline int write(T x, Args... args) {
return write(x) + write(args...);
}
struct node;
typedef node* list;//接下来写起来方便
struct node {
int val; list last;//val为奶牛的编号,last为上一头奶牛的位置
node(int val = 0, list last = 0): val(val), last(last){}//构造函数
};
char opt;
int n, x;
list a[N];
int main() {
#ifdef ONLINE_JUDGE
fin = stdin;
fout = stdout;
#else
fin = fopen("P6182.in", "rb");
fout = fopen("P6182.out", "wb");
#endif
a[0] = new node(3216037), a[read(n)] = new node(-1, a[0]), ++n;//a[0]甚至可以用1******7代替,read(n)的返回值为1,这里简写
for (int i = 2; i <= n; ++i) {//为了方便操作,将n加1,并且i从2开始
read(opt);
if (opt == 's') a[i] = new node(a[i - 1]->last->val, a[i - 1]->last->last);//删除
else {
read(x); if (opt == 'a') a[i] = new node(x, a[i - 1]);//插入
else a[i] = new node(a[x]->val, a[x]->last);//可持久化
}
write(a[i]->val, '\n');
}
return 0;
}